makalah statistik dan probabilitas lengkap
PROBABILITAS DAN
STATISTIK
 |
| Add caption |
DISUSUN OLEH :
RIAN HIDAYAT
RIFQI MUAFIQ
ROYADI PUTRA LUMBANBATU
SUHARTATI
S NINGRUM
DAFTAR ISI
ABSTRAK...................................................................................................................................................
BAB I
PENDAHULUAN.....................................................................................................................
1.1 LATAR
BELAKANG..........................................................................................................
BAB II
PEMBAHASAN............................................................................................................................
2.1 PENGERTIAN PROBABILITAS
..................................................................................
2.2 PENDEKATAN PERHITUNGAN
PROBABILITAS..............................................
2.3 KONSEP FREKUENSI
RELATIF...............................................................................
2.4 ATURAN DASAR
PROBABILITAS...........................................................................
2.5 FAKTORIAL,PERMUTASI ,KOMBINASI.................................................................
2.6 PENELITIAN PADA
PELEMPARAN DADU,UANG LOGAM
DAN PENGAMBILAN KELERENG
PADA TEORI BAYES......................................
2.7 MANFAAT PROBABILITAS DALAM
PENELITIAN................................................
2.8 PENGERTIAN
STATISTIK...............................................................................................
2.9 JENIS – JENIS
STATISTIK.................................................................................................
2.10 PENELITIAN STATISTIK
PENGGUNAAN TENAGALISTRIKAN
TAHUN 2014........................................................................................................................
2.11 PENGERTIAN
DATA..........................................................................................................
2.12 METODE PENGUMPULAN DATA...................................................................................
2.13 PENYAJIAN DATA................................................................................................................
2.14 POPULASI DAN SAMPEL...............................................................................................
2.15 SKALA PENGUKURAN ....................................................................................................
2.16 VARIABEL
PENELITIAN................................................................................................
BAB III
PENUTUP.........................................................................................................................................
3.1 KESIMPULAN..........................................................................................................................
3.2
SARAN......................................................................................................................................
DAFTAR
PUSTAKA.......................................................................................................................................
ABSTRAKSI
Statistik
merupakan suatu ilmu tentang pengumpulan, penyusunan, penganalisaan dan
penafsiran data dalam bentuk angka untuk tujuan pembuatan suatu keputusan yang
lebih baik di dalam menghadapi ketidakpastian. Singkatnya statistika adalah
ilmu yang berkenaan dengan data..Sebagaian besar konsep dasar statistika
mengasumsikan teori probabilitas. Probabilitas atau peluang adalah cara untuk
mengungkapkan pengetahuan atau kepercayaan bahwa suatu kejadian akan berlaku
atau telah terjadi. Probabilitas suatu kejadian adalah angka yang menunjukkan
kemungkinan terjadinya suatu kejadian. Nilainya diantara 0 dan 1. Kejadian yang
mempunyai nilai 1 adalah kejadian yang pasti terjadi atau telah terjadi.
Misalnya matahari yang masih terbit di timur sampai sekarang. Sedangkan
kejadian yang mempunya nilai probabilitas 0 adalah kejadian yang mustahil atau
tidak mungkin terjadi. Misalnya seekor kambing melahirkan seekor sapi. Dalam
statistika dikenal pula dengan konsep probabilitas atau peluang. Probabilitas
adalah angka yang menjukkan kemungkinan terjadinya suatu kejadian dimasa
mendatang akan terjadi, peluang ini hanya memuati nilai antara 0 sampai dengan
~. Konsep statsitika probabilitas biasanya dinyatakan dengan pecahan seperti :
½ ; ¼ ; ¾ ataupun dalam bentuk desimal seperti: 0,25 ; 0,50 ataupun 0,75. Salah
satu contoh yang sering digunakan dalam menerangkan konsep probabilitas adalah
dengan pelemparan mata uang. Jika kita melempar mata uang, maka kenungkinan
sisi gambar untuk muncul sama dengan kemungkinan munculnya sisi angka. Dengan
demikian probabilitas munculnya sisi gambar yaitu ½ atau 0,5 dan demikian pula
denga probabilitas sisi angka. Begitu juga denga probabilitas mata dadu
kemungkinan munculnya salah satu angka adalah 1/6. Didalam modul ini diambil
beberapa contoh dalam konsep statistika probabilitas, yaitu dari percobaan
pelemparan dadu, pelemparan uang logam dan pengambilan kelereng. Dar i
percobaan-percobaan tersebut dilakukan beberapa pelemparan untuk mendapatkan
hasil yang bervariasi. Data - data yang telah terkumpul tersebut kemudian
diolah sehingga dapat ditampilkan dan dapat dianalisa serta ditarik
kesimpulannya.
BAB I
PENDAHULUAN
1.1 .Latar belakang
Sampai
saat ini statistika merupakan alat dan juga metode analisis yang dipakai untuk
mengevaluasi data yang pada akhirnya akan diperoleh suatu kesimpulan
berdasarkan sampel yang ada. Dari semua alat analisa, konsep probailitas
merupakan salah satu alat analisis yang mempunyai peran sangat penting untuk
memecahkan masalah dalam kehidupan sehari-hari mulai dari bidang ilmiah sampai
pada masalah-masalah kecil, seperti masuk kantor atau tidak, kareana awan tebal
kemungkinan akan hujan deras dan banjir, dan sebagainya. Meskipun kejadian-kejadian
tersebut tidak pasti, tetapi kita bisa melihat fakta-fakta yang ada untuk
menuju derajat kepastian atau derajat keyakinan bahwa sesuatu akan terjadi.
Derajat atau tingkat kepastian atau keyakinan dari munculnya hasil percobaan
statistik disebut Probabilitas (Peluang), yang dinyatakan dengan P.
Probabilitas sering diterjemahkan sebagai peluang atau kebolehkejadian, yaitu
peristiwa yang didefinisikan sebagai peluang proses terjadinya sesuatu, baik
disengaja (eksperimentasi) atau tidak.
Pada
makalah ini, akan dipelajari mengenai probabilitas yang menyatakan suatu nilai
kejadian yang dapat terjadi lagi. Konsep probabilitas ialah suatu bagian ilmu
dari statistika yang dapat meramalkan kejadian yang dapat terjadi lagi di masa
mendatang , peluang ini hanya memuat nilai antara 0 sampai dengan 1.
Dalam
pembuatan modul konsep probabilitas ini akan dijelaskan beberapa hal tentang
peluang dan bagaimana mencari nilai peluang, diantaranya peluang irisan dua
kejadian, peluang paduan dua kejadian, peluang bersyarat dan menerapkan konsep
kaidah bayes serta menganalisa sampai dengan menarik kesimpulan dari hasil
nilai peluang yang telah didapat.
b.Identifikasi masalah
Mencari
nilai peluang munculnya mata dadu yang dilemparkan.
Mencari
nilai peluang munculnya permukaan 4 koin yang dilemparkan secara bersama-sama.
Mencari
nilai peluang munculnya kelerang yang di ambil.
Mencari
nilai peluang pengambilan kelereng dengan metode kaidah bayes.
c.Perumusan masalah
Dalam
penyusunan Modul ini data-data yang kami ambil untuk dianalisa, diolah dan
ditampilkan adalah sebagai berikut:
Bagaimana
melakukan pengolahan data peluang dalam pelemparan mata dadu, pelemparan uang
logam dan pengambilan kelereng ?
Bagaimana
melakukan pengolahan dan penganalisaan terhadap data-data yang telah diolah
agar, mendapatkan kesimpulan mengenai data-data tersebut ?
d. Pembatasan masalah
Mengolah
perhitungan data peluang dalam pelemparan dadu, pelemparan koin, dan
pengambilan kelereng.
Pelemparan
mata dadu dengan melakukan 2x percobaan. Yang pertama dengan melakukan
percobaan pelemparan sebanyak 55x dan yang kedua pelemparan sebanyak 70x.
Pelemparan
uang logam. Percobaan pada uang logam dilakukan dengan menggunakan 4 buah uang
logam dengan percobaan sebanyak 50x pelemparan uang logam. Sehingga 1x pelemparan
didapatkan 4 peluang. Yaitu peluang yang sama untuk angka dan gambar.
Pengambilan kelereng. Kelereng
yang digunakan pada percobaan ini ada menggunakan 3 warna kelereng, yaitu
Merah, Kuning dan Hijau. Dan ada beberapa kelereng yang diberi tanda. Sehingga
peluang yang ada semakin sempit. Pada percobaan ini dilakukan 2x, yaitu 25x
pengambilan dan 35x pengambilan.
e. Tujuan penelitian
Memahami
konsep dasar probabilitas.
Memahami
peluang irisan dua kejadian, peluang gabungan serta peluang bersyarat.
Memahami
pengaruh probabilitas dalam menentukan hasil dari setiap percobaan yang
dilakukan.
BAB II
PEMBAHASAN
2.1 Pengertian Probabilitas
Secara
umum probabilitas merupakan peluang bahwa sesuatu akan terjadi.Secara lengkap
probabilitas didefinisikan sebagai berikut :
“Probabilitas”
ialah suatu nilai yang digunakan untuk mengukur tingkat terjadinya suatu
kejadian acak.”
Dalam
mempelajari probabilitas, ada tiga kata kunci yang harus diketahui:
1.
Eksperimen,
2.
Hasil (outcome)
3.
Kejadian atau peristiwa (event)
Contoh
:
Dari
eksperimen pelemparan sebuah koin. Hasil (outcome) dari pelemparan sebuah koin
tersebut adalah “MUKA” atau “BELAKANG”.
Kumpulan
dari beberapa hasil tersebut dikenal sebagai kejadian (event).
Probabilitas
biasanya dinyatakan dengan bilangan desimal (seperti 0,50 ; 0,25 atau 0,70)
atau bilangan pecahan (seperti ).
Nilai
dari probabilitas berkisar antara 0 dan 1. Semakin dekat nilai
probabilitas
ke nilai 0, semakin kecil kemungkinan suatu kejadian akan terjadi.
Sebaliknya
semakin dekat nilai probabilitas ke nilai 1 semakin besar peluang suatu
kejadian akan terjadi.
2.2 Pendekatan Perhitungan Probabilitas
Ada
dua pendekatan dalam menghitung probabilitas yaitu pendekatan yang bersifat
objektif dan subjektif. Probabilitas objektif dibagi menjadi dua, yaitu:
1.
Pendekatan Klasik
Probabilitas
diartikan sebagai hasil bagi dari banyaknya peristiwa yang dimaksud dengan
seluruh peristiwa yang mungkin menurut pendekatan klasik, probabilitas
dirumuskan :
keterangan
:
P(A)
= probabilitas terjadinya kejadian A.
x
= peristiwa yang dimaksud.
n
= banyaknya peristiwa.
Contoh
:
Dua
buah dadu dilempar ke atas secara bersamaan. Tentukan probabilitas munculnya
angka berjumlah 5.
Penyelesaian
:
Hasil
yang dimaksud (x) = 4, yaitu (1,4), (4,1), (2,3). (3,2)
Hasil
yang mungkin (n) = 36, yaitu (1,1), (1,2), (1,3). ….., (6,5), (6,6).
2.3 Konsep Frekuensi Relatif
Menurut
pendekatan frekuensi relatif, probabilitas diartikan sebagai proporsi waktu
terjadinya suatu peristiwa dalam jangka panjang, jika kondisi stabil atau
frekuensi relatif dari suatu peristiwa dalam sejumlah besar percobaan.
Nilai
probabilitas ditentukan melalui percobaan, sehingga nilai probabilitas itu
merupakan limit dari frekuensi relatif peristiwa tersebut.
Menurut pendekatan frekuensi
relatif, probabilitas dirumuskan :
keterangan
:
P(Xi)
= probabilitas peristiwa i.
Fi
= frekuensi peristiwa i.
n
= banyaknya peristiwa yang bersangkutan.
Contoh
:
Dari
hasil ujian statistik, 65 mahasiswa STMIK MDP, didapat nilai-nilai sebagai
berikut.
X
F
5,0
11
6,5
14
7,4
13
8,3
15
8,8
7
9,5
5
x
= nilai statistik.
Tentukan
probabilitas salah seorang mahasiswa yang nilai statistiknya 8,3.
Penyelesaian
:
Frekuensi
mahasiswa dengan nilai 8,3 (f) = 15
Jumlah
mahasiswa (n) = 65.
Probabilitas Subjektif
Menurut
pendekatan subjektif, probabilitas diartikan sebagai tingkat kepercayaan
individu yang didasarkan pada peristiwa masa lalu yang berupa terkaan saja.
Contoh
:
Seorang
direktur akan memilih seorang supervisor dari empat orang calon yang telah
lulus ujian saringan. Keempat calon tersebut sama pintar, sama lincah, dan
semuanya dapat dipercaya. Probabilitas tertinggi (kemungkinan diterima) menjadi
supervisor ditentukan secara subjektif oleh sang direktur.
Dari
pengertian-pengertian tersebut, dapat disusun suatu pengertian umum mengenai
probabilitas, yaitu sebagai berikut Probabilitas adalah suatu indeks atau nilai
yang digunakan untuk menentukan tingkat terjadinya suatu kejadian yang bersifat
random (acak).
Oleh
karena probabilitas merupakan suatu indeks atau nilai maka probabilitas
memiliki batas-batas yaitu mulai dari 0 sampai dengan 1 ( 0 £ P £ 1).
a.
Jika P = 0, disebut probabilitas kemustahilan, artinya kejadian atau peristiwa
tersebut tidak akan terjadi.
b.
Jika P = 1, disebut probabilitas kepastian, artinya kejadian atau peristiwa
tersebut pasti terjadi.
c.
Jika 0 < P < 1, disebut probabilitas kemungkinan, artinya kejadian atau
peristiwa tersebut dapat atau tidak dapat terjadi.
2.4 Aturan Dasar Probabilitas
Aturan Penjumlahan :
Untuk
menerapkan aturan penjumlahan ini, harus dilihat jenis kejadiannya apakah
bersifat saling meniadakan atau tidak saling meniadakan.
Kejadian
Saling Meniadakan :
Dua
peristiwa atau lebih disebut saling meniadakan jika kedua atau lebih peristiwa
itu tidak dapat terjadi pada saat yang bersamaan. Jika peristiwa A dan B saling
meniadakan, probabilitas terjadinya peristiwa tersebut adalah
P(A
atau B) = P(A) + P(B) atau
P(A
¨ B) = P(A) + P(B)
Contoh :
Sebuah
dadu dilemparkan ke atas, peritiwanya adalah
A
= peristiwa mata dadu 4 muncul.
B
= peristiwa mata dadu lebih kecil dari 3 muncul.
Tentukan
probabilitas dari kejadian berikut !
-
Mata dadu 4 atau lebih kecil dari 3 muncul!
Penyelesaian
:
P(A)
= 1/6 P(B) = 2/6
P(A
atau B) = P(A) + P(B) = 1/6 + 2/6 = 0,5
P(B)
= 14/36
P(A
B) = 0
P(A
atau B) = P(A) + P(B) – P(A ˙ B)
=
1/36 + 14/36 – 0
=
0,42
Aturan Perkalian :
Dalam
konsep probabilitas, aturan perkalian diterapkan secara berbeda menurut jenis
kejadiannya. Ada dua jenis kejadian dalam hal ini, yaitu kejadian tak bebas dan
kejadian bebas.
1.
Kejadian Tak Bebas
Dua
peristiwa atau lebih disebut kejadian tidak bebas apabila peristiwa yang satu
dipengaruhi atau tergantung pada peritiwa lainnya. Probabilitas peristiwa tidak
saling bebas dapat pula dibedakan atas tiga macam, yaitu probabilitas
bersyarat, gabungan, dan marjinal.
a.
Probabilitas Bersyarat :
Probabilitas
bersyarat peristiwa tidak saling bebas adalah probabilitas terjadinya suatu
peristiwa dengan syarat peristiwa lain harus terjadi dan peristiwa-peristiwa
tersebut saling mempengaruhi.
Jika
peristiwa B bersyarat terhadap A, probabilitas terjadinya periwtiwa tersebut
adalah P(B/A) dibaca probabilitas terjadinya B dengan syarat peristiwa A
terjadi.
Contoh
:
Sebuah
kotak berisikan 11 bola dengan rincian :
5
buah bola putih bertanda +
1
buah bola putih bertanda –
3
buah bola kuning bertanda +
2
buah bola kuning bertanda –
Seseorang
mengambil sebuah bola kuning dari kotak
-
Berapa probabilitas bola itu bertanda +?
Penyelesaian
:
Misalkan
: A = bola kuning
B+
= bola bertanda positif
B-
= bola bertanda negatif.
P(A)
= 5/11
P(B+A)
= 3/1
b. Probabilitas Gabungan :
Probabilitas
gabungan peritiwa tidak saling bebas adalah probabilitas terjadinya dua atau
lebih peristiwa secara berurutan (bersamaan) dan peristiwa-peristiwa itu saling
mempengaruhi.
Jika
dua peristiwa A dan B gubungan, probabilitas terjadinya peristiwa tersebut
adalah P(A dan B) = P(A ˙ B) = P(A) x P(B/A)
Jika
tiga buah peristiwa A, B, dan C gabungan, probabilitas terjadinya adalah P(A ˙
B ˙ C) = P(A) x P(B/A) x P(C/A ˙ B)
Contoh :
Dari
satu set kartu bridge berturut-turut diambil kartu itu sebanyak 2 kali secara
acak. Hitunglah probabilitasnya kartu king (A) pada pengambilan pertama dan
as(B) pada pengambilan kedua, jika kartu pada pengambilan pertama tidak
dikembalikan !
Penyelesaian
:
(A)
= pengambilan pertama keluar kartu king.
P(A)
= 4/52
(B/A)
= pengambilan kedua keluar kartu as
P(B/A)
= 4/51
P(A
˙ B) = P(A) x P(B/A) = 4/52 x 4/51 = 0,006
c. Probabilitas Marjinal :
Probabilitas
marjinal peristiwa tidak saling bebas adalah probabilitas terjadinya suatu
peristiwa yang tidak memiliki hubungan dengan terjadinya peristiwa lain dan
peristiwa tersebut saling mempengaruhi. Jika dua peristiwa A adalah marjinal,
probabilitas terjadinya peristiwa A tersebut adalah
P(A)
= SP(B ˙ A) = SP(Ai) x P(B/Ai), i = 1, 2, 3, …..
Contoh
:
Sebuah
kotak berisikan 11 bola dengan rincian :
5
buah bola putih bertanda +
1
buah bola putih bertanda –
3
buah bola kuning bertanda +
2
buah bola kuning bertanda –
Tentukan
probabilitas memperoleh sebuah bola putih !
Penyelesaiannya :
Misalkan
: A = bola putih
B+
= bola bertanda positif
B-
= bola bertanda negatif
P(B+A)
= 5/11
P(B-A)
= 1/11
P(A)
= P(B+A) + P(B-A) = 5/11 + 1/11 = 6/11
2. Kejadian Bebas :
Dua
kejadian atau lebih dikatakan merupakan kejadian bebas apabila terjadinya
kejadian tersebut tidak saling mempengaruhi. Dua kejadian A dan B dikatakan
bebas, kalau kejadian A tidak mempengaruhi B atau sebaliknya.
Jika
A dan B merupakan kejadian bebas, maka P(A/B) = P(A) dan P(B/A) = P(B)
P(A
˙ B) = P(A) P(B) = P(B) P(A)
Contoh
:
Satu
mata uang logam Rp. 50 dilemparkan ke atas sebanyak dua kali. Jika A1 adalah
lemparan pertama yang mendapat gambar burung(B), dan A2 adalah lemparan kedua
yang mendapatkan gambar burung(B), berapakah P(A1+A2)!
Penyelesaian
:
Karena
pada pelemparan pertama hasilnya tidak mempengaruhi pelemparan kedua dan P(A1)
= P(B) = 0,5 dan P(A2) = P(B) = 0,5, maka P(A1+A2) =P(A1) P(A2) = P(B) P(B) =
0,5 x 0,5 = 0,25.
Rumus
Bayes :
Jika
dalam suatu ruang sampel (S) terdapat beberapa peristiwa saling lepas, yaitu
A1, A2, A3, …., A n yang memiliki probabilitas tidak sama dengan noldan bila
ada peritiwa lain (misalkan X) yang mungkin dapat terjadi pada
peristiwa-peristiwa A1, A2, A3, …., A
maka probabilitas terjadinya
peristiwa-peristiwa A1, A2, A3, ….,A
dengan
diketahui peristiwa X tersebut adalah
Contoh
:
Tiga
kotak masing-masing memiliki dua laci. Didalam laci-laci tersebut terdapat
sebuah bola. Didalam kotak I terdapat bola emas, dalam kotak II terdapat bola
perak, dan dalam kotak III terdapat bola emas dan perak. Jika diambil sebuah
kotak dan isinya bola emas, berapa probabilitas bahwa laci lain berisi bola
perak?
Penyelesaian
:
Misalkan
:
A1
peristiwa terambil kotak I
A2
peristiwa terambil kotak II
A3
peristiwa terambil kotak III
X
peristiwa laci yang dibuka berisi bola emas
Kotak
yang memenuhi pertanyaan adalah kotak III (P(A3/X)).
P(A1)
= 1/3 P(X/A1) = 1
P(A2)
= 1/3 P(X/A2) = 0
P(A3)
= 1/3 P(X/A3) = ½
Permutasi Dan Kombinasi
Pembicaraan
mengenai permutasi dan kombinasi selalu berkaitan dengan prinsip dasar
membilang dan faktorial.
Prinsip
Dasar Membilang :
Jika
kejadian pertama dapat terjadi dalam n 1 cara, kejadian kedua dalam n 2 cara,
demikian seterusnnya, sampai kejadian k dalam n k cara, maka keseluruhan
kejadian dapat terjadi dalam :
n1
x n2 x …x n k cara
Contoh :
Seorang
pengusaha ingin bepergian dari Jakarta ke Ujungpandang melalui Surabaya. Jika
Jakarta – Surabaya dapat dilalui dengan tiga cara dan Surabaya – Ujungpandang
dapat dilalui dengan dua cara, ada berapa cara pengusaha tersebut dapat tiba di
Ujungpandang melalui Surabaya?
Penyelesaian
:
misalkan
:
Dari
Jakarta ke Surabaya (n1) = 3 cara.
Dari
Surabaya ke Ujung pandang (n2) = 2 cara.
Cara
pengusaha tersebut dapat tiba di Ujungpandang melalui Surabaya adalah :
n1
x n2 = 3 x 2 = 6 cara.
2.4 * Faktorial
Faktorial
adalah perkalian semua bilangan bulat positif (bilangan asli) terurut mulai
dari bilangan 1 sampai dengan bilangan bersangkutan atau sebaliknya.
Faktorial
dilambangkan: “!”.
Jika
: n = 1,2, …., maka :
n!
= n(n – 1)(n – 2) ….x 2 x 1 = n(n –1)!
Contoh
:
Tentukan
nilai factorial dari bilangan berikut
a.
5!
b.
3! X 2!
c.
6!/4!
Penyelesaian
:
a.
5! = 5 x 4 x 3 x 2 x 1 = 120
b.
3! X 2! = 3 x 2 x 1 x 2 x 1 = 12
** Permutasi
a.
Pengertian Permutasi :
Permutasi
adalah suatu penyusunan atau pengaturan beberapa objek ke dalam suatu urutan
tertentu.
Contoh
:
Ada
3 objek, yaitu ABC. Pengaturan objek-objek tersebut ialah ABC, ACB, BCA, BAC,
CAB, CBA yang disebut permutasi. Jadi, permutasi 3 objek menghasilkan enam
pengaturan dengan cara yang berbeda.
b. Rumus-rumus Permutasi :
Permutasi
dari m objek seluruhnya tanpa pengembalian : mPm = m!
Contoh
:
Pada
suatu tempat terdapat 4 buku matematika yang berbeda. Buku itu akan disusun
pada sebuah rak buku. Berapa cara susunan yang mungkin dari buku-buku
matematika dapat disusun.
Penyelesaian
:
Buku-buku
matematika dapat disusun dalam :
4P4
= 4! = 4 x 3 x 2 x 1 = 24 cara.
Permutasi
sebanyak x dari m objek tanpa pengembalian :
Contoh
:
Dari
empat calon pimpinan sebuah perusahaan, misalkan A, B, C, D hendak dipilih
seorang ketua, seorang sekretaris, dan seorang bendahara.
Berapa
cara keempat calon tersebut dipilih?
Penyelesaian
:
Misalkan :
Dari
Jakarta ke Surabaya (n1) = 3 cara.
Dari
Surabaya ke Ujungpandang (n2) = 2 cara.
Cara
pengusaha tersebut dapat tiba di Ujungpandang melalui Surabaya adalah :
n1x
n2 = 3 x 2 = 6 cara.
*** Kombinasi
a.
Pengertian Kombinasi :
Kombinasi
adalah suatu penyusunan beberapa objek tanpa memperhatikan urutan objek
tersebut
Contoh
:
Ada
4 objek, yaitu : A, B, C, D. Kombinasi 3 dari objek itu adalah ABC, ABD, ACD,
BCD. Setiap kelompok hanya dibedakan berdasarkan objek yang diikutsertakan,
bukan urutannya. Oleh karena itu :
ABC
= ACB = BAC = BCA = CAB = CBA
ABD
= ADB = BAD = BDA = DAB = DBA
ACD
= CAD = ADC = CDA = DAC = DCA
BCD
= BDC = CBD = CDB = DBC = DCB
b. Rumus-rumus Kombinasi :
Kombinasi
x dari m objek yang berbeda :
m!
mCx = -------------- ; m ‡ x
(m
– x)!.x!
Contoh
:
Dari
5 pemain bulu tangkis, yaitu A, B, C, D, dan E hendak dipilih dua orang untuk
pemain ganda. Berapa banyak pemain ganda yang mungkin terbentuk?
Penyelesaian :
M
= 5 dan x = 2
5!
5C2
= ---------------- = 10
(5
– 2)! . 2!
2.6 Manfaat Probabilitas Dalam Penelitian
Manfaat
probabilitas dalam kehidupan sehari-hari adalah membantu kita dalam mengambil suatu
keputusan, serta meramalkan kejadian yang mungkin terjadi. Jika kita tinjau
pada saat kita melakukan penelitian, probabilitas memiliki beberapa fungsi
antara lain;
1.
Membantu peneliti dalam pengambilan keputusan yang lebih tepat. Pengambilan
keputusan yang lebih tepat dimagsudkan tidak ada keputusan yang sudah pasti
karena kehidupan mendatang tidak ada yang pasti kita ketahui dari sekarang,
karena informasi yang didapat tidaklah sempurna. 5:6, sedangkan hasil sensus
pada tahun 2010 menunjukan hasil perbandingan jumlah penduduk berjenis kelamin
pria berbanding jumlah penduduk berjenis kelamin wanita adalah 5:7. Maka
pemerintah dapat mengambil keputusan bahwa setiap tahunnya dari tahun 2000
hingga 2010 jumlah wanita berkembang lebih pesat daripada jumlah penduduk pria.
Menghitung Probabilitas atau
Peluang Suatu Kejadian
Jika
tadi kita hanya memperhatikan peluang suatu kejadian secara
kualitatip,
hanya memperhatikan apakkah kejadian tersebut memiliki peluang besar akan
terjadi atau tidak. Disini kita akan membahas nilai dari probabilitas suatu
kejadian secara kuantitatip. Kita bias melihat apakah suatu kejadian berpotensi
terjadi ataukah tidak.
Misalkan
kita memiliki sebuah dadu yang memiliki muka gambar
dan angka,jika koin tersebut kita
lemparkan keatas secara sembarang, maka kita memiliki 2 pilihan yang sama besar
dan kuat yaitu peluang munculnya angka dan peluang munculnya gambar. Jika kita
perhatikan secara seksama, pada satu koin hanya terddiri dari satu muka gambar
dan satu muka angka, maka peluang munculnya angka dan gambar adalah sama kuat
yaitu ½. 1 menyatakan hanya satu dari muka pada koin yang mungkin muncul, entah
itu gambar maupun angka sedangkan 2 menyatakan banyaknya kejadian yang mungkin
terjadi pada pelemparan koin, yaitu munculnya gambar + munculnya angka.
Jika
kita berbicara tidak lagi 2 kejadian yaitu menyangkut banyak kejadian yang
mungkin terjadi, mengingat dan dari hasil pengumpulan dan penelitian data
diperoleh suatu rumus sebagai berikut. Jika terdapat N peristiwa, dan n A dari
N peristiwa tersebut membentuk kejadian A, maka probabilitas A adalah :
P(A)
= n A/N
Dimana
:
n
A= banyaknya kejadian
N=
kejadian seluruhnya/peristiwa yang mungkin terjadi
Contoh.
Suatu
mata uang logam yang masing-masing sisinya berisi gambar dan angka dilemparkan
secara bebas sebanyak 1 kali.
Berapakah
probabilitas munculnya gambar atau angka?
Jawab
:
n=1,
N=2
P
(gambar atau angka)=
P
(gambar atau angka)=1/2 atau 50%
Dapat
disimpulkan peluang munculnya gambar atau angka adalah sama besar.
Contoh 2.
Berapa
peluang munculnya dadu mata satu pada satu kali pelemparan?
Jika
kita tinjau pada sebuah dadu hanya memiliki 1 buah mata dadu bermata 1,
sedangkan pada dadu terdapat 6 mata yaitu mata 1 sampai mata 6.
Maka:
P(A)
= n A/N = 1/6
Berikut
merupakan aturan dalam probabilitas
1.
Jika n = 0 makka peluang terjadinya suatu kejadian pada keadaan ini adalah
sebesar P(A) = 0 atau tidak mungkin terjadi.
2.
Jika n merupakan semua anggota N maka pro
3.
Probabilitas suatu kejadian memiliki rentangan nilai
4.
Jika E menyatakan bukan peristiwa E maka berlaku.
babilitasnya
adalah satu,
atau
kejadian tersebut pasti akan terjadi.
Dari pengolahan data peluang yang
telah dilakukan berdasarkan teori dan secara praktek dalam pengumpulan data,
diperoleh nilai nilai peluang yang benilai di antara 0 sampai dengan 1. Hal ini
secara teori dikatakan bahwa nilai peluang tidak melebihi angka 1, jika nilai
peluang melebihi 1 berarti terdapat perhitungan data peluang yang tidak benar.
2.7 * PENELITIAN PELEMPARAN DADU
Peluang
munculnya mata dadu pada percobaan pertama sebanyak 55x adalah:
Mata
dadu 1 = 5/55
Mata
dadu 2 = 8/55
Mata
dadu 3 = 6/55
Mata
dadu 4 = 16/55
Mata
dadu 5 = 9/55
Mata
dadu 6 = 11/55
Peluang
munculnya mata dadu pada percobaan kedua sebanyak 70x adalah:
Mata
dadu 1 = 7/70
Mata
dadu 2 = 10/70
Mata
dadu 3 = 15/70
Mata
dadu 4 = 12/70
Mata
dadu 5 = 9/70
Mata
dadu 6 = 17/70
Tabel perbandingan hasil nilai
peluang pada dadu.
No
Peluang Teori Praktek
55x
70x
1
P(M) 0,50 0,35 0,44
2
P(N) 0,50 0,64 0,56
3
P(O) 0,50 0,36 0,44
4
P(M∩N) 0,17 0,15 0,14
5
P(M∩O) 0,33 0,20 0,31
6
P(N∩O) - - -
7
P(M∪N) 0,83 0,84 0,87
8
P(M∪O) 0,67 0,51 0,59
9
P(N∪O) 1 1 1
10
P(M∩N∩O) - - -
11
P(M∪N∪O) 1 1 1
Dari
tabel diatas terlihat perbedaan nilai peluang antara secara teori dan praktek
yang tidak jauh atau nilai peluang pada praktek mendekati nilai peluang secara
teori. Dari tabel tersebut terlihat pada praktek pelemparan dadu sebanyak 55x
dan 70x peluang yang akan muncul kembali (terjadi lagi) yang paling kecil
adalah P(M∩N).
** PENELITIAN
PELEMPARAN UANG LOGAM
Nilai
peluang pada pelemparan 4 buah uang logam yang diberi nomer 1-4 dan dilemparkan
secara bersama-sama sebanyak 50x adalah sebagai berikut:
No
Peluang Hasil Teori Hasil Praktek 50x
1
P(M) 0,50 0,50
2
P(N) 0,50 0,44
3
P(O) 0,50 0,44
4
P(P) 0,50 0,44
5
P(M') 0,50 0,50
6
P(N') 0,50 0,56
7
P(O') 0,50 0,56
8
P(P') 0,50 0,56
9
P(M∩N) 0,25 0,26
10
P(M∩O) 0,25 0,28
11
P(M∩P) 0,25 0,22
12
P(N∩O) 0,25 0,26
13
P(N∩P) 0,25 0,16
14
P(O∩P) 0,25 0,16
15
P(M∩N') 0,25 0,24
16
P(M∩O') 0,25 0,22
17
P(M∩P') 0,25 0,28
18
P(N∩O') 0,25 0,18
19
P(N∩P') 0,25 0,28
20
P(O∩P') 0,25 0,28
21
P(M'∩N') 0,25 0,32
22
P(M'∩O') 0,25 0,34
23
P(M'∩P') 0,25 0,32
24
P(N'∩O') 0,25 0,38
25
P(N'∩P') 0,25 0,28
26
P(O'∩P') 0,25 0,28
27
P(M∩N∩O∩P) 0,06 0,06
28
P(M'∩N'∩O'∩P') 0,06 0,12
29
P(M∪N) 0,75 0,68
30
P(M∪O) 0,75 0,66
31
P(M∪P) 0,75 0,72
32
P(N∪O) 0,75 0,62
33
P(N∪P) 0,75 0,72
34
P(O∪P) 0,75 0,72
35
P(M∪N') 0,75 0,82
36
P(M∪O') 0,75 0,84
37
P(M∪P') 0,75 0,78
38
P(N∪O') 0,75 0,82
39
P(N∪P') 0,75 0,72
40
P(O∪P') 0,75 0,72
41
P(M'∪N') 0,75 0,74
42
P(M'∪O') 0,75 0,72
43
P(M'∪P') 0,75 0,78
44
P(N'∪O') 0,75 0,74
45
P(N'∪P') 0,75 0,84
46
P(O'∪P') 0,75 0,84
47
P(M∪N∪O∪P) 0,94 0,88
48
P(M'∪N'∪O'∪P') 0,94 0,94
49
P(M|N) 0,50 0,59
50
P(O|M) 0,50 0,64
51
P(P|M) 0,50 0,50
52
P(N|O) 0,50 0,59
53
P(N|P) 0,50 0,36
54
P(O|P) 0,50 0,36
55
P(M|N') 0,50 0,43
56
P(M|O') 0,50 0,39
57
P(M|P') 0,50 0,50
58
P(N|O') 0,50 0,32
59
P(N|P') 0,50 0,50
60
P(O|P') 0,50 0,50
61
P(M'|N') 0,50 0,57
62
P(M'|O') 0,50 0,61
63
P(M'|P') 0,50 0,57
64
P(N'|O') 0,50 0,68
65
P(N'|P') 0,50 0,50
66
P(O'|P') 0,50 0,50
Dari tabel diatas dapat ditarik
sebuah analisa bahwa secara teoritis nilai peluang untuk setiap anggota bagian
(M,N,O,P,M',N',O',P') mempunyai nilai yang sama. Dan secara toritis juga nilai
peluang untuk irisan 2 kejadian, irisan 4 kejadian (jenis sama), gabungan 2
kejadian, gabungan 4 kejadian untuk setiap jenis anggota (angka dan gambar)
mempunyai nilai yang sama, begitupun dengan nilai peluang bersyarat secara
teoritis juga mempunyai hasil nilai yang sama.
Namun
secara praktek berbeda dengan nilai peluang yang diperoleh secara teori tetapi
tidak mengalami perbedaan yang signifikan, nilai-nilai peluang pada praktek
selalu mendekati nilai peluang pada teori baik pada peluang untuk setiap
anggota bagian, irisan 2 kejadian, irisan 4 kejadian (jenis sama), gabungan 2
kejadian, gabungan 4 kejad ian untuk setiap jenis anggota (angka dan gambar),
maupun peluang bersyarat.
Dari
hasil nilai peluang pada praktek
pelemparan 50x yang diperoleh dapat diambil sebuah analisa bahwa peluang
untuk setiap anggota bagian yang paling terkecil adalah P(N), P(O), P(P) dengan
nilai 0,44 dan yang terbesar adalah P(N'), P(O'), P(P') dengan nilai 0,56.
Untuk peluang irisan 2 kejadian yang terkecil adalah P(N∩P) dan P(O∩P) dengan
nilai 0,16, sedangkan yang terbesar adalah P(N'∩O') dengan nilai 0,38. Untuk
peluang irisan 4 kejadian yang kecil yaitu P(M∩N∩O∩P) dengan nilai 0,06.
Sedangkan
untuk peluang gabungan 2 kejadian yang terkecil adalah P(N∪O) dengan nilai 0,62,
lalu yang terbesar adalah P(M∪O'),
P(N'∪P'), dan P(O'∪P') dengan nilai
0,84. Untuk peluang gabungan 4 kejadian
dengan jenis yang sama (angka/gambar) yang kecil adalah peluang untuk gabungan
4 kejadian angka P(M∪N∪O∪P) dengan nilai 0,88.
Selanjutnya untuk peluang bersyarat yang terkecil adalah P(N|O') dengan nilai
0,32 dan yang terbesar adalah P(N'|O') dengan nilai 0,68.
Pengambilan
Kelereng
Tabel
perbandingan hasil
No
Peluang Teori
15x
Praktek
25x
35x
1
P(KM | T) 0,43 0,30 0,29
2
P(KK | T) 0,29 0,20 0,29
3
P(KH | T) 0,29 0,50 0,43
4
P(KM | TT) 0,25 0,20 0,29
5
P(KK | TT) 0,50 0,47 0,14
6
P(KH | TT) 0,25 0,33 0,57
Dari tabel yang telah disusun
untuk perbandingan hasil peluang pengambilan kelereng secara teori dan paraktek
ternyata diperoleh nilai-nilai peluang yang hampir sama atau mendekati seperti
pada P(KK | T), dan P(KM | TT) dengan nilai peluang antara 0,20 sampai dengan
0,30.
Namun
untuk P(KH | T) pada praktek 25x dan 35x nilainya menalami perbedaan yang
sgnifikan dengan teori 15x yaitu 0,29 dan untuk P(KK | TT) juga mengalami perbedaan
nilai hasil peluang yang cukup signifikan, pada teori 15x dengan nilai 0,50
,pada paktek 35x dengan nilai 0,14. Begitu juga untuk P(KH | TT) mengalami
perbedaan nilai hasil peluang yang cukup signifikan, pada teori 15x dengan
nilai 0,25, pada praktek 25x dengan nilai 0,33, dan pada praktek 35x dengan
nilai 0,57.
*** Pengambilan
Kelereng Dengan Teori Bayes
Dalam
teori bayes dilakukan pengambilan kelereng sebanyak 30x, lalu untuk menentukan
nilai peluangnya menggunakan nilai peluang jk dengan nilai 1/3.
No Peluang Hasil
1
P(KM) 0,33
2
P(KK) 0,33
3
P(KH) 0,33
4
P(T|KM) 0,20
5
P(T|KK) 0,70
6
P(T|KH) 0,80
7
P(TT|KM) 0,60
8
P(TT|KK) 0,50
9
P(TT|KH) 0,20
10
P(T) 0,60
11
P(KM|T) 0,11
12
P(KK|T) 0,39
13
P(KH|T) 0,44
14
P(TT) 0,43
15
P(KM|TT) 0,47
16
P(KK|TT) 0,39
17
P(KH|T) 0,16
Pada perhitungan peluang
pengambilan kelereng dengan kaidah bayes digunakan rumus peluang bersyarat
untuk memperoleh hasil nilai peluangnya. Diperoleh nilai peluang yang terkecil
adalah P(KH|T) dan P(KM|TT) dengan nilai 0,16 dan 0,11, dan peluang yang
terbesar adalah P(T|KH) dengan nilai 0,80.
2.8 pengertian statistik.
Statistika adalah pengetahuan yang berkaitan dengan metode, teknik atau
cara mengumpulkan, mengolah, menganalisis dan menginterprestasikan data untuk
disajikan secara lengkap dalam bentuk yang mudah dipahami penggunan.
Berdasarkan latar belakang diatas penulis/ penyusun ingin mengetahui lebih
jauh tentang statistik termaksud juga tentang jenis-jenis berdasarkan metode
yang dipakai di dalam system statistic ini.
Metode statistik
Metode statistik
merupakan ilmu pengetahuan yang meliputi segala metode guna mengumpulkan,
mengolah, menyajikan dan menganalisis data kuantitatif secara deskriptif.
Fokus kegiatan adalah pengumpulan dan penataan data serta penggunaan
pengukuran yang sifatnya menyederhanakan.
Menurut Croxton dan Cowden definisi tersebut lebih menekankan pada teknik
mengumpulkan, mengolah, menyederhanakan, menyajikan dan menganalisis data
kuantitatif secara deskriptif untuk memberikan deskripsi terhadap suatu
peristiwa. Oleh sebab itu dinamakan metode statistik deskriptif.
Selanjutnya Croxton dan Cowden memberi definisi statistik yang lebih luas
yakni metode guna mengumpulkan, mengolah, menyajikan, menganalisis dan
menginterpretasi data yang berwujud angka-angka.
Kata interpretasi bermakna penarikan kesimpulan dari hasil analisis yang
dilakukan atas dasar data kuantitatif yang terbatas. Artinya metode statistik
tidak hanya memberikan teknik pengumpulan, pengolahan, penyajian dan analisis
data semata melainkan juga memberikan teknik penarikan kesimpulan tetntang ciri
populasi dari hasil pengukuran yang dilakukan terhadap sampel yang telah
dipilih secara random.
Metode penarikan kesimpulan umum tersebut sesungguhnya merupakan inti dari
statistik modern yang kemudian populer dengan sebutan statistik inferensial.
Bidang kajian/ cakupan statistik deskriptif :
Distribusi frekuensi
Penyajian grafik, bagan dan diagram
Pengukuran tendensi sentral/ pemusatan (mean, median, modus)
Pembagian distribusi (kuartil, desil, persentil)
Variabilitas (range, mean deviasi, standar deviasi, Z score )
Angka indeks
Time series (deret waktu atau data berkala)
Bidang Kajian statistik Inferensial :
Probabilitas/ teori kemungkinan
Distribusi teoritis
Sampling dan distribusi sampling
Studi estimasi (penaksiran pada tingkat populasi )
Uji hipotesis
Analisis korelasional dan uji signifikansi
Analisis regresi untuk peramalan.
Berdasarkan bentuk distribusi parameternya statistik dibagi menjadi :
Statistik parametrik : bagian statistik di mana parameter populasi
diketahui mengikuti distribusi normal dan memiliki varians yang homogen.
Statistik non parametrik : Jenis statistik
di mana parameter populasi tidak mengikuti distribusi normal atau
distribusi bebas (free distribution) dan varians tidak perlu homogen.
Statistika dibedakan berdasarkan jenisnya menjadi dua yaitu Statistika Deskriptif dan Statistika Inferensia.
Statistika deskriptif adalah statistika yang berkaitan dengan metode atau cara medeskripsikan, menggambarkan, menjabarkan atau menguraikan data. Statistika deskripsi mengacu pada bagaimana menata, menyajikan dan menganalisis data, yang dapat dilakukan misalnya dengan menentukan nilai rata-rata hitung, median, modus, standar deviasi atau menggunakan cara lain yaitu dengan membuat tabel distribusi frekuensi dan diagram atau grafik.
Statistika inferensia adalah statistika yang berkaitan dengan cara penarikan kesimpulan berdasarkan data yang diperoleh dari sampel untuk menggambarkan karakteristik dari suatu populasi. Dengan demikian dalam statistika inferensia data yang diperoleh dilakukan generalisasi dari hal yang bersifat kecil (khusus) menjadi hal yang bersifat luas (umum).
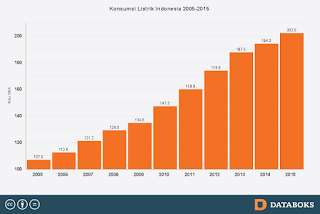
2.10 penelitian statistik penggunaan listrik di indonesia
tahun 2014
Sektor ketenagalistrikan merupakan salah satu leading sector dalam
menunjang perekonomian dan pembangunan nasional. Listrik sudah menjadi
kebutuhan vital bagi masyarakat dalam kehidupan sehari-hari. Saat ini, hampir
semua peralatan rumah tangga membutuhkan listrik dalam penggunaannya seperti
pesawat televisi, kulkas, air conditioner (AC), mesin cuci, laptop, komputer,
handphone dan lain-lain. Selain itu, listrik juga berperan penting bagi dunia
industri dan jasa dalam proses produksi untuk dapat menggerakkan perekonomian.
Tidak heran, demand terhadap listrik meningkat setiap tahunnya sementara
pasokan listrik sendiri sangat terbatas. Hal ini menyebabkan berbagai wilayah
di tanah air sering sekali mengalami pemadaman listrik bergilir terutama di daerah-daerah
pinggiran dan pedalaman. Lebih jauh, saat ini kondisi yang sangat
memprihatinkan adalah masih banyak daerah di tanah air yang sama sekali belum
teraliri listrik.
Gambar konsumsi listrik di indonesia pertahun
2015-2016. Sumber: internet/Databoks
Rasio elektrifikasi di Indonesia secara keseluruhan bila dibandingkan
dengan negara-negara kawasan masih cukup tertinggal. Pada tahun 2014, rasio
elektrifikasi Indonesia masih sekitar 84,3 persen menempati peringkat ke-6 di
ASEAN setelah Singapura yaitu 100 persen, Malaysia 99,4 persen, Thailand 99,3
persen, Vietnam 97,3 persen, dan Philipina sebesar 89,7 persen. Selain itu,
konsumsi listrik penduduk per kWh per kapita Indonesia juga masih cukup rendah
bila dibandingkan dengan negara-negara tetangga tersebut. Rata-rata konsumsi
listrik Indonesia pada 2014 sebesar 0,7 kWh per kapita. Terdapat perbedaan yang
cukup signifikan bila dibandingkan dengan Singapura yaitu sebesar 8,4 kWh per
kapita, Malaysia 4,3 kWh per kapita, Thailand 2,3 kWh per kapita dan Vitenam 1,1 kWh per kapita.
Gambar statistik
penggunaan listrik di asia. Sumber: internet
Di Indonesia sendiri, dilihat dari statistik yang dikeluarkan oleh
pemerintah, terdapat kesenjangan yang cukup lebar antara pulau Jawa dan luar
pulau Jawa dalam penyediaan listrik. Hal ini dapat dilihat dari perbandingan
rasio elektrifikasi antara Sumatera, Jawa-Bali dan Indonesia Timur. Pada tahun
2009, rasio elektrifikasi pulau Jawa adalah 67,6%, Sumatera 62,7%, dan
Indonesia Timur hanya sebesar 50,6%. Sedangkan pada tahun 2014, rasio
elektrifikasi di pulau Jawa meningkat menjadi 87%, Sumatera menjadi 85,5%,
sementara untuk Indonesia Timur menjadi 73,9%. Kondisi ini juga mencerminkan
adanya perbedaan yang cukup signifikan terutama antara Jawa dan Indonesia Timur
dalam penyediaan tenaga listrik yang adil dan merata bagi masyarakat.
Berdasarkan data statistik yang dirilis oleh PLN, ada enam golongan
pelanggan yang menikmati aliran listrik antara lain
·
kelompok rumah
tangga,
·
kelompok bisnis,
·
kelompok industri,
·
transportasi atau penerangan jalan.
Dari berbagai kelompok tersebut,
kelompok terbesar pengguna listrik adalah rumah tangga.
Pertumbuhan konsumen rumah tangga
setiap tahunnya meningkat rata-rata 3,5 juta pelanggan, diikuti oleh sektor bisnis
140 ribu pelanggan, sektor publik 82 ribu pelanggan, dan sektor industri
meningkat rata-rata 2 ribu pelanggan setiap tahunnya. Adanya peningkatan
tersebut yang tidak diimbangi dengan pertumbuhan kapasitas pembangkit berakibat
kepada pasokan listrik yang semakin terbatas.
Kondisi kelistrikan yang belum optimal menimbulkan berbagai kerugian dan
masalah bagi masyarakat dan pengguna listrik. Dampak kurangnya ketersediaan
listrik sangat dirasakan oleh kalangan masyarakat di wilayah-wilayah remote
area yang belum teraliri listrik maupun wilayah-wialyah yang pasokan listriknya
terbatas. Kurangnya pasokan listrik menyebabkan banyak rumah tangga belum bisa
menikmati listrik untuk kebutuhan sehari-hari seperti penerangan.
Di daerah-daerah yang pasokan listriknya terbatas, masyarakat harus
mengalami pemadaman listrik berkali-kali setiap harinya. Selain merugikan
masyarakat karena waktu operasional yang kurang, pemadaman yang dilakukan
secara rutin dan tiba-tiba juga dapat merugikan konsumen akibat kerusakan
peralatan rumah tangga karena korsleting arus listrik. Kondisi seperti ini
sangat sering terjadi terutama di daerah-daerah luar pulau Jawa yang pasokannya
terbatas seperti sebagian Sumatera dan Kalimantan, serta Indonesia Timur.
2.11 PENGERTIAN
DATA
Dalam statistika dikenal beberapa jenis data. Data dapat berupa angka dapat
pula bukan berupa angka. Data berupa angka disebut data kuantitatif dan data
yang bukan angka disebut data kualitatif.
Berdasarkan nilainya dikenal dua jenis data kuantitatif yaitu data diskrit
yang diperoleh dari hasil perhitungan dan data kontinue yang diperoleh dari
hasil pengukuran.
Menurut sumbernya data dibedakan menjadi dua jenis yaitu data interen
adalah data yang bersumber dari dalam suatu instansi atau lembaga pemilik data
dan data eksteren yaitu data yang diperoleh dari luar.
Data eksteren dibagi menjadi dua jenis yaitu data primer dan data sekunder.
Data primer adalah data yang langsung dikumpulkan oleh orang yang
berkepentingan dengan data tersebut dan data sekunder adalah data yang tidak
secara langsung dikumpulkan oleh orang yang berkepentingan dengan data
tersebut.
Dalam statistika dikenal beberapa
jenis data. Data dapat berupa angka dapat pula bukan berupa angka. Data berupa
angka disebut data kuantitatif dan data yang bukan angka disebut data
kualitatif.Berdasarkan nilainya dikenal dua jenis data kuantitatif yaitu data diskrit yang diperoleh dari hasil perhitungan dan data kontinue yang diperoleh dari hasil pengukuran.
Menurut sumbernya data dibedakan menjadi dua jenis yaitu data interen adalah data yang bersumber dari dalam suatu instansi atau lembaga pemilik data dan data eksteren yaitu data yang diperoleh dari luar.
Data eksteren dibagi menjadi dua jenis yaitu data primer dan data sekunder. Data primer adalah data yang langsung dikumpulkan oleh orang yang berkepentingan dengan data tersebut dan data sekunder adalah data yang tidak secara langsung dikumpulkan oleh orang yang berkepentingan dengan data tersebut.
2.12 CARA PENGUMPULAN DATA
Untuk memperoleh data yang benar dan dapat dipertanggung jawabkan keabsahannya, data harus dikumpulkan dengan cara dan proses yang benar. Terdapat beberapa cara atau teknik untuk mengumpulkan data yaitu :
1) Wawancara (interview)
Yaitu cara untuk mengumpulkan data dengan mengadakan tatap muka secara langsung. Wawancara harus dilakukan dengan memakai suatu pedoman wawancara yang berisi daftar pertanyaan sesuai tujuan yang ingin dicapai.
Ada dua jenis wawancara yaitu wawancara berstruktur (structured interview) dan wawancara takberstruktur (unstructured interview). Wawancara berstruktur adalah wawancara yang jenis dan urutan dari sejumlah pertanyaannya sudah disusun sebelumnya, sedangkan waw
ancara takberstruktur adalah wawancara yang tidak secara ketat ditentukan sebelumnya. Wawancara takberstruktur lebih fleksibel karena pertanyaannya dapat dikembangkan meskipun harus tetap pada pencapaian sasaran yang telah ditentukan.
Ciri-ciri pertanyaan yang baik adalah :
a. Sesuai dengan masalah atau tujuan penelitian.
b. Jelas dan tidak meragukan.
c. Tidak menggiring pada jawaban tertentu.
d. Sesuai dengan pengetahuan dan pengalaman orang yang diwawancarai.
e. Pertanyaan tidak boleh yang bersifat pribadi.
Kelebihan dari wawancara adalah data yang diperlukan langsung diperoleh sehingga lebih akurat dan dapat dipertanggung jawabkan.
Kekurangannya adalah tidak dapat dilakukan dalam skala besar dan sulit memperoleh keterangan yang sifatnya pribadi.
2) Kuesioner (angket)
Adalah cara mengumpulkan data dengan mengirim atau menggunakan kuesioner yang berisi sejumlah pertanyaan.
Kelebihannya adalah dapat dilakukan dalam skala besar, biayanya lebih murah dan dapat memperoleh jawaban yang sifatnya pribadi.
Kelemahannya adalah jawaban bisa tidak akurat, bisa jadi tidak semua pertanyaan terjawab bahkan tidak semua lembar jawaban dikembalikan.
3) Observasi (pengamatan)
Adalah cara mengumpulkan data dengan mengamati obyek penelitian atau kejadian baik berupa manusia, benda mati maupun gejala alam. Data yang diperoleh adalah untuk mengetahui sikap dan perilaku manusia, benda mati atau gejala alam.
Kebaikan dari observasi adalah data yang dieroleh lebih dapat dipercaya.Kelemahannya adalah bisa terjadi kesalahan interpretasi terhadap kejadian yang diamati.
4) Tes dan Skala Obyektif
adalah cara mengumpulkan data dengan memberikan tes kepada obyek yang diteliti. Cara ini banyak dilakukan pada tes psikologi untuk mengukur karakteristik kepribadian seseorang. Beberapa contoh tes skala obyektif yaitu :
a. Tes kecerdasan dan bakat.
b. Tes kepribadian.
c. Tes sikap.
d. Tes tentang nilai.
e. Tes prestasi belajar, dsb.
·
METODE PROYEKTIF
Adalah
cara mengumpulkan data dengan mengamati atau menganalisis suatu obyek melalui
ekspresi luar dari obyek tersebut dalam bentuk karya lukisan atau tulisan.
Metode ini dipakai dalam psikologi untuk mengetahui sikap, emosi dan
kepribadian seseorang. Kelemahan dari metode ini adalah obyek yang sama dapat
disimpulkan berbeda oleh pengamat yang berbeda.
2.13 PENYAJIAN
DATA
Secara garis besar ada dua cara penyajian data yaitu dengan tabel dan
grafik. Dua cara penyajian data ini saling berkaitan karena pada dasarnya
sebelum dibuat grafik data tersebut berupa tabel. Penyajian data berupa grafik
lebih komunikatif.
Dilihat dari waktu pengumpulannya, dikenal dua jenis data yaitu : Cross
section data adalah data yang dikumpulkan pada suatu waktu tertentu. Data
berkala adalah data yang dikumpulkan dari waktu ke waktu. Dengan data berkala
dapat dibuat garis kecenderungan atau trend.
1) Penyajian data dengan table
Tabel atau daftar merupakan kumpulan angka yang disusun menurut kategori
atau karakteristik data sehingga memudahkan untuk analisis data.
Ada tiga jenis tabel yaitu :
a. Tabel satu arah atau satu
komponen adalah tabel yang hanya terdiri atas satu kategori atau karakteristik
data. Tabel berikut ini adalah contoh tabel satu arah.
b. Tabel dua arah atau dua komponen adalah
tabel yang menunjukkan dua kategori atau dua karakteristik. Tabel berikut ini
adalah contoh tabel dua arah
2.Penyajian data dengan grafik/diagram
Penyajian data dengan grafik dianggap lebih komunikatif karena dalam waktu
singkat dapat diketahui karakteristik dari data yang disajikan.
Terdapat beberapa jenis grafik yaitu :
·
Grafik garis
·
Grafik Batang
Populasi adalah keseluruhan pengamatan atau obyek yang menjadi perhatian sedangkan Sample adalah bagian dari populasi yang menjadi perhatian.
Populasi dan sample masing-masing mempunyai karakteristik yang dapat diukur atau dihitung. Karakteristik untuk populasi disebut parameter dan untuk sample disebut statistik.
Contoh parameter adalah mean (µ), standar deviasi ( ), proporsi (P) dan koefisien korelasi ( ), sedangkan statistik adalah nilai rata-rata ( ), standar deviasi (s), proporsi (p) dan koefisien korelasi (r).
Populasi dibedakan menjadi dua jenis yaitu :
Populasi orang atau individu adalah keseluruhan orang atau individu (dapat pula berupa benda-benda) yang menjadi obyek perhatian.
Populasi
data adalah populasi yang terdiri atas keseluruhan karakteristik yang menjadi
obyek perhatian.
Sampel juga dibedakan menjadi dua
jenis yaitu :Sampel orang atau individu adalah sampel yang terdiri atas orang-orang (dapat pula berupa benda-benda) yang merupakan bagian dari populasinya yang menjadi obyek perhatian.
Sampel data adalah sebagaian karakteristik dari suatu populasi yang menjadi obyek perhatian.
Meskipun populasi merupakan gambaran yang ideal, tetapi sangat jarang penelitian dilakukan memakai populasi. Pada umumnya yang dipakai adalah sample. Ada beberapa alasan mengapa penelitian dilakukan menggunakan sample :
1. Waktu yang diperlukan untuk mengumpulkan data lebih singkat.
2. Biaya lebih murah.
3. Data yang diperoleh justru lebih akurat.
4. Dengan statistika inferensia dapat dilakukan generalisasi.
2.15 SKALA PENGUKURAN
Salah satu aspek penting dalam
memahami data untuk keperluan analisis terutama statistika inferensia adalah
Skala Pengukuran. Secara umum terdapat 4 tingkat/jenis skala pengukuran yaitu :1. Skala nominal
Adalah
skala yang hanya mempunyai ciri untuk membedakan skala ukur yang satu dengan
yang lain. Contoh skala nominal seperti tabel dibawah ini :
Jenis
dan jumlah buah-buahan yang diproduksi suatu daerah pada tahun 1998
|
Jenis buah
|
jumlah
|
|
Apel
|
2 ton
|
|
Mangga
|
1,5 ton
|
|
Durian
|
4 ton
|
|
Anggur
|
6,5 ton
|
sumber: Data buatan
2. Skala Ordinal
Adalah skala yang selain mempunyai ciri untuk membedakan juga mempunyai
ciri untuk mengurutkan pada rentang tertentu. Contoh skala ordinal seperti
tabel dibawah ini.
Penilaian Anggota Kelompok Belajar Teknik Elektro UNIVERSITAS PAMULANG.
|
Kategori Nilai
|
Banyaknya Mahasiswa
|
|
Istimewa
|
5 orang
|
|
Baik
|
15 orang
|
|
Cukup
|
5 orang
|
|
Kurang
|
3 orang
|
|
Kurang Sekali
|
0 orang
|
Sumber: Data buatan
2.16 VARIABEL PENELITIAN
Pengertian
Variabel Penelitian
Variabel
merupakan sesuatu yang menjadi objek pengamatan penelitian, sering juga disebut
sebagai faktor yang berperan dalam penelitian atau gejala yang akan diteliti.
Menurut Kerlinger (2006: 49), variabel adalah konstruk atau sifat yang akan
dipelajari yang mempunyai nilai yang bervariasi. Kerlinger juga mengatakan
bahwa variabel adalah simbol/lambang yang padanya kita letakan sebarang nilai
atau bilangan. Menurut Sugiyono (2009: 60), variabel adalah segala sesuatu yang
berbentuk apa saja yang ditetapkan oleh peneliti untuk dipelajari sehingga
diperoleh informasi tentang hal tersebut, kemudian ditarik kesimpulannya.
Selanjutnya menurut Suharsimi Arikunto (1998: 99), variabel penelitian adalah
objek penelitian atau apa yang menjadi perhatian suatu titik perhatian suatu
penelitian. Bertolak dari pendapat para ahli di atas maka dapat disimpulkan
bahwa variabel penelitian adalah suatu atribut dan sifat atau nilai orang,
faktor, perlakuan terhadap obyek atau kegiatan yang mempunyai variasi tertentu
yang ditetapkan oleh peneliti untuk dipelajari dan kemudian ditarik
kesimpulannya.
Jenis-Jenis Variabel Penelitian
Variabel
dapat dikelompokkan menurut beragam cara, namun terdapat tiga jenis tiga jenis
pengelompokkan variabel yang sangat penting dan mendapatkan penekanan.
Karlinger, (2006: 58) antara lain:
Variabel bebas dan variabel terikat
Variabel
bebas sering disebut independent, variabel stimulus, prediktor, antecedent.
Variabel bebas adalah variabel yang mempengaruhi atau yang menjadi sebab
perubahannya atau timbulnya variabel terikat. Variabel terikat atau dependen
atau disebut variabel output, kriteria, konsekuen, adalah variabel yang
dipengaruhi atau yang menjadi akibat, karena adanya variabel bebas. Variabel
terikat tidak dimanipulasi, melainkan diamati variasinya sebagai hasil yang
dipradugakan berasal dari variabel bebas. Biasanya variabel terikat adalah
kondisi yang hendak kita jelaskan.
Dalam
eksperimen-eksperimen, variabel bebas adalah variabel yang dimanipulasikan
(“dimainkan”) oleh pembuat eksperimen. Misalnya, manakala peneliti di bidang
pendidikan mengkaji akibat dari berbagai metode pengajaran, peneliti dapat
memanipulasi metode sebagai (variabel bebasnya) dengan mengggunakan berbagai
metode. Dalam penelitian yang bersifat tidak eksperimental, yang dijadikan
variabel bebas ialah yang “secara logis” menimbulkan akibat tertentu terhadap
suatu variabel terikat. Contohnya, dalam penelitian tentang merokok dan kanker
paru-paru, merokok (yang memang telah dilakukan oleh banyak subyek) merupakan
variable bebas, sementara kangker paru-paru merupakan akibat dari merokok atau
sebagai variabel terikat. Jadi variabel bebas adalah variabel penyebab,
sadangkan variabel terikat yang menjadi akibatnya. Dalam bidang pendidikan
variabel terikat yang paling lazim adalah, misalnya prestasi, atau “hasil
belajar”. Untuk mengetahui prestasi belajar peserta didik, peneliti memiliki
sejumlah besar kemungkinan variabel bebasnya, antara lain: kecerdasan, kelas
sosial, metode pembelajaran, tipe
kepribadian, tipe motivasi (imbalan/hadiah dan hukuman), sikap terhadap
sekolah, suasana kelas dan seterusnya. Untuk lebih mudah dipahami berikut ini
ditampilkan skema mengenai penjelasan di atas.
Variabel aktif dan variabel atribut
Variabel
aktif adalah variabel bebas yang dimanipulasi. Sebarang variabel yang
dimanipulasikan merupakan variabel aktif. Misalnya peneliti memberikan
penguatan positif untuk jenis kelakuan tertentu dan melakukan hal yang berbeda
terhadap kelompok lain atau memberikan instruksi yang berlainan pada kedua
kelompok tersebut atau peneliti menggunakan metode pembelajaran yang berbeda,
atau memberikan imbalan kepada subyek-subyek dalam kelompok lain, atau menciptakan
kecemasan dengan instruksi-instruksi yang meresahkan, maka peneliti secara
aktif memanipulasi variabel
metode, penguatan, dan kecemasan.
Variabel atribut adalah yang tidak
dapat dimanipulasi atau kata lain variabel yang sudah melekat dan merupakan
ciri dari subyek penelitian. Misalnya: Intelegensi, bakat jenis kelamin, status
sosial-ekonomi, sikap, daerah geografis suatu wilayah, dan seterusnya. Ketika
kita melakukan penelitian atau kajian subyek-subyek penelitian kita sudah
membawa variabel-variabel (atribut-atribut) itu. Yang membentuk individu atau
subyek penelitian tersebut adalah lingkungan, keturunan, dan situasi-situasi
lainnya.
Perbedaan variabel aktif dan variabel
atribut ini bersifat umum. Akan tetapi variabel atribut dapat pula menjadi
variabel aktif. Ciri ini memungkinkan untuk penelitian relasi “yang sama”
dengan cara berbeda. Misalnya kita dapat mengukur kecemasan subyek. Jelas bahwa
dalam hal ini kecemasan merupakan atribut. Akan tetapi kita dapat pula
memenipulasi kecemasan. Kita dapat menumbuhkan kecemasan dengan tingkat yang
berbeda, dengan mengatakan kepada subyek-subyek yang termasuk dalam kelompok
eksperimen (kelompok yang diteliti) bahwa yang harus mereka kerjakan sulit,
maka tingkat kecerdasan mereka akan diukur dan masa depan mereka tergantung
pada skor tes itu. Sedangkan kepada subyek lainya dipesan bahwa kerja
sebaik-baiknya tetapi santai saja; hasil tes tidak terlalu penting dan sama
sekali tidak mempengaruhi hari depan mereka.
Variabel kontinu dan variabel kategori
Sebuah variabel kontinu memiliki
sehimpunan harga yang teratur dalam suatu cakupan (range) tertentu. Arti
defenisi ini ialah:
1.
Harga-harga suatu variabel kontinu
mencerminkan setidaknya suatu urutan peringkat. Harga yang lebih besar untuk
variabel itu berarti terdapatnya lebih banyak sifat tertentu (sifat yang
dikaji) yang dikandungnya, dibandingkan dengan variabel dengan harga yang lebih
murah. Misalnya, harga-harga yang diperoleh dari suatu skala untuk mengukur
ketergantungan (depedensi) mengungkapkan ketergantungan dengan kadar yang
berbeda-beda, yakni mulai dari tinggi, menengah/sedang, sampai rendah.
2.
Ukuran-ukuran kontinu dalam
penggunaan nyata termuat dalam suatu range, dan tiap individu mendapatkan skor
yang ada dalam range tersebut. Misalnya suatu skala untuk mengukur
ketergantungan mungkin memiliki range dari 1 hingga 7.
3.
Secara teoritis terdapat himpunan
harga atau nilai yang tak berhingga banyaknya dalam range itu. Demikianlah maka
skor seseorang individu mungkin sekali adalah 4,72 dan bukan 4 atau 5.
Variabel kategori variabel yang
berkaitan dengan suatu jenis pengukuran yang dinamakan pengukuran nominal.
Dalam pengukuran nominal terdapat dua himpunan bagian (subset) atau lebih
yang merupakan bagian dari himpunan (set) obyek yang diukur. Individu-individu
dikategorisasikan berdasarkan pemilikan ciri-ciri tertentu yang merupakan
penentu suatu himpunan bagian. Jadi persoalah variabel ini adalah antara “ya”
atau “tidak”. Contoh paling mudah adalah variabel kategori dikotomis: jenis
kelamin, republik-demokrat, kulit putih-kulit hitam, dan sebagainya. Politomi,
yakni pilihan (partisi) cukup lazim terdapat khususnya dalam sosiologi dan ilmu
ekonomi: anutan agama, pendidikan, kewarganegaraan, pilihan pekerjaan, dan seterusnya.
Syarat-syarat yang dituntut variabel
kategori dan variabel nominal, adalah semua anggota himpunan bagain dipandang
sama. Misalnya, kalau variabel itu adalah anutan agama, semua penganut
protestan adalah sama; semua penganut katolik adalah sama; dan semua penganut
“lain-lain” pun sama. Jika seorang agama katolik, dia dimasukan dalam kategori
“katolik” dan diberi angka (nomor) “1” dalam katergori tersebut. Variabel ini
bersifat “demokratis” artinya, tidak mengenal tatanan peringkat atau ungkapan “lebih
besar” maupun “lebih kecil” daripada di antara kategorinya. Semua anggota
kategori memiliki nilai atau harga sama, yakni:
Ungkapan variabel kualitatif
kadang-kadang digunakan untuk menunjuk variabel-variabel kategori ini, khusunya
dikotomi, barangkali juga untuk mengkontraskanya dengan variabel kuatitatif
(variabel kontinu). Penggunaan ungkapan itu mencerminkan adanya gagasan yang
agak menyimpang mengenai hakikat variabel. Variabel selalu dapat
dikuantisasikan; jika tidak demikian, tentunya bukanlah variabel.
Sebelummnya dijelaskan bahwa konstruk
adalah hal-hal yang tak teramati (non observable) sedangkan defenisi variabel
secara operasional adalah hal-hal yang teramati (observable). Kerlinger (2006:
66) menambahkan bahwa hal yang dimaksud adalah “variabel laten”. Variabel laten
adalah suatu utuhan obyek (entity) tak teramati yang diduga melandasi variabel
amatan. Peneliti cenderung lebih berminat pada variabel-variabel laten,
daripada relasi antara variabel-variabel amatan; sebab peneliti berupaya menjelaskan
fenomena dan relasinya.
Istilah-istilah lain untuk
mengungkapkan gagasan yang kira-kira sama misalnya konstruk disebut
dengan variabel intervensi (intervening variabel). Variabel intervensi
adalah istilah yang dibuat untuk menunjuk pada proses-proses psikologis yang
internal dan tak teramati, yang pada gilirannya mengacu pada perilaku. suatu
variabel intervensi ini “hanya ada di otak peneliti” tidak dapat dilihat,
didengar, atau diraba; disimpulkan dari perilaku.
Kegunaan dan Kriteria Variabel Penelitian
1. Kegunaan
Variabel
1.
Untuk mempersiapkan alat dan metode
pengumpulan data
2.
Untuk mempersiapkan metode
analisis/pengolahan data
3.
Untuk pengujuian hipotesis
2. Variabel
penelitian yang baik
1.
Relevan dengan tujuan
penelitian
2.
Dapat diamati dan dapat diukur
3.
Dalam suatu penelitian, variabel
perlu diidentifikasi, diklasifikasi, dan didefenisikan secara operasional
dengan jelas dan tegas agar tidak menimbulkan kesalahan dalam pengumpulan dan
pengolahan data serta dalam pengujian hipotesis.
BAB
III
PENUTUP
3.1 KESIMPULAN
Dari jabaran
diatas dapat kita simpulkan bahwa:
1.
Probabilitas adalah kemungkinan yang terjadi
berdasarkan keadaan yang telah ada.
2.
Probabilitas ada dua macam, yaitu: Probabilitas a
priori dan Probabilitas relative frekuensi.
3.
tindakan yang kita ambil berdasarkan resiko yang
mungkin timbul dari pilihan kita berkaitan dengan probabilitas yang ada
- Metode statistik prosedur –
prosedur atau cara-cara penyajian dan penafsiran data. Penyajiannya
meliputi : penyajian, pengorganisasian, peringkasan dan penyajian data.
Sedangkan penafsiran data meliputi : pengdugaan, pengujian dugaan dan
penarikan kesimpulan.
- Jenis Metode Statistik ada 2 yaitu :
- Statistik deskriptif (Descriptive
Statistics) adalah metode pengumpulan, peringkasan dan penyajian data.
Descriptive bersifatmemberi gambaran.
- Statistik Inferensia (Inferential
Statistics) adalah metode statistik peramalan, pendugaan dan penarikan
kesimpulan. Inferential bersifat melakukan generalisasi (penarikan
kesimpulan.)
3.2 saran
Statistic dan probabilitas adalah suatu ilmu pengetahuan sangat dibutuhkan
untuk perkembangan dunia banyak sekali orang ingin mengetahui cabang ilmu ini
sehingga banyak yang mengetahui ilmu statistik namun karena kesukaran sehingga
banyak yang terkadang enggan atau malas untuk mempelajari ilmu ini sebenarnya
statistik mudah untuk dipelajari yang
penting ada niat dari kita untuk mau mendalami ilmu ini pasti akan tahu dan
paham sebagai ntang ilmu statistik ini. Dengan demikian saran kami kami sebagai
penyusun sebagai mahasiswa fakultas ekonomi agar lebih memberikan sedikit
motivasi dalam diri untuk mempelajari ilmu ini “ilmu yang lain juga” agar
kedepannya apabila telah selesai dapat mempertanggunga jawabkan semua ilmu yang
kita dapatkan. Sekian terima kasih.

mantap.....
BalasHapus